Pas facile la physique

Lorsque le navire s'incline sous l'effet d'une force extérieure, le centre de carène se déplace de Co en C1,( on considère que pour de petites inclinaisons, le centre de carène décrit une portion d'arc de cercle de centre m, point que l'on appelle métacentre de carène. On peut l'assimiler à un centre de rotation instantané relatif à une inclinaison donnée. On nomme le point H point métacentrique. On notera que H est à une distance finie lorsque l'inclinaison est nulle.)
Le rayon de ce cercle peut être calculé par la formule de Bouguer :
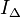est le moment quadratique de la surface de flottaison par rapport à son axe d'inclinaison (exprimé en m⁴) et le volume de carène (exprimé en m³).
Il se forme un couple de redressement de moment tendant à faire retrouver au navire sa position initiale droite. P est le déplacement et GZ le bras de levier.
On peut remarquer que plus G sera haut et se rapprochera de m, plus le bras de levier de redressement GZ sera faible. Lorsque GZ sera nul il n'existera pas de bras de levier de redressement, le navire continuera à s'incliner, ou du moins sera en équilibre instable. Lorsque G est au-dessus de m, le bras de levier sera inclinant et augmentera l'inclinaison, jusqu'à atteindre une position d'équilibre qui peut être à 180° (à l'envers).
La position du centre de gravité du navire (G) doit être surveillée. Un chargement dans les hauts fera monter G, un chargement dans les bas fera descendre G. Un navire commencera donc, de manière générale, par charger dans les fonds avant de charger dans les compartiments supérieurs. La valeur de GM est sujette à des réglementations (Solas), entre autres: un minimum de l'ordre de 0,30 m voire 0,45 m pour certains navires.
Dans le triangle GZH rectangle en Z: , et aussi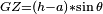
Le moment du couple de redressement peut donc s'écrire:.

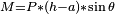"C'est qui qu'a pris les piles de la calculatrice?"